数学的美

数学可以是“美”的吗？这个问题可能会让很多不是学数学的人皱眉头，因为欣赏数学中的美，常常比欣赏一幅画或一首歌更虚幻。对于大多数人来说，数学公式往往与枯燥无味、繁琐复杂联系在一起。然而，有研究表明，数学的美不仅仅是数学家的独特视角，它实际上也可以激活大脑中欣赏艺术和音乐的相同区域。这表明，数学的美和绘画、音乐的美有很多共同之处。如果你可以从一幅图画或者一首歌中感受到美，那你也有可能可以体会到数学中的美。

英国曾经有研究人员请了十几位数学家为一系列数学公式和数学方程打分。研究人员在数学家观看这些公式的时候对数学家的大脑进行扫描。结果，他们发现，当数学家认为某个公式优美的时候，他们的大脑内侧眶额皮质活动显著增加，而这正是我们在欣赏一幅美丽的画作或聆听一首动人的音乐时活跃的大脑区域。

对数学家而言，他们比一般的人可以更容易看到或者体会到数学方程式中与美相关的属性。例如，最简单直接的，是一个公式在形态上是否简单、对称、优雅。在上面提到的研究中，被数学家认为最美丽的方程式包括毕达哥拉斯恒等式

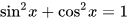
和欧拉恒等式

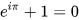
欧拉恒等式曾被人称为 “数学中的蒙娜丽莎”。因为它简洁优美地将五个最基本的数学常数联系在了一起：自然数 $e$、圆周率 $\pi$、虚数 $i$，以及和数学的产生相关的两个最基本的数：$0$ 和 $1$。美国数学史家威廉·邓纳姆曾这样描述欧拉公式里的五个常数：如果你想做加法，你需要 $0$；如果你想做乘法，你需要 $1$；如果你想做微积分，你需要 $e$；如果你想做几何，你需要 $\pi$；如果你想做复分析，你需要 $i$。

相反，一些复杂且难以理解的方程式则被认为是“丑陋”的，比如黎曼Zeta函数方程：

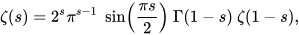
其表面繁杂怪异的形态让绝大多数人光是看看它就会头疼不已。

但是，和其他人对艺术和音乐的欣赏一样，数学家的审美显然也不仅仅是感官刺激的产物。主观意识在数学家的审美评判中有很重要的地位。比如数学家对欧拉恒等式的喜好，和他们对相关的常数的了解有关。

事实上，如果你有足够的数学知识，你也许能够超越一个方程表面的形态，在更深的层次上体验到它的“美”。例如，上面被作为研究对象的数学家认为是“丑陋”的黎曼Zeta函数方程，对熟悉其中的Zeta函数的人而言，也许就不会那么“丑陋”的了。

黎曼Zeta函数，也叫欧拉-黎曼Zeta函数，在分析数论中有重要的地位，在统计、物理中也有应用。如果我们对 Zeta 函数的定义，对级数、积分、复变函数以及数论的相关历史有所了解，这些枯燥的符号也许就会生动起来、故事化起来。例如，Zeta 函数 $\zeta(s)$ 是一个来自于无穷个简单的分式相加的复函数：

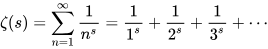
而著名的欧拉乘积公式，把Zeta 函数和我们大家都熟知的素数关联起来：

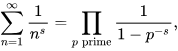
这个公式的左边就是Zeta函数，包含加法，整数，简单的分式。而右边，却是由所有素数构成的简单分式的乘积！这种运算上的对偶、相似，外形上的对称、简洁、优雅，关系上的神奇、出人意外，不能不让人产生由衷的赞叹，为之心旷神怡。

如果我们进一步了解黎曼Zeta 函数方程中的Gamma函数和Zeta函数的关系，黎曼Zeta函数方程表面的“丑陋”就可能被这个方程所揭示的内涵关系的“奇妙”所代替。

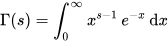
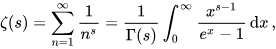
如果你还有机会看到黎曼zeta函数方程的证明，也许你会进一步被数学的符号和运算体系的优雅所感动。

到这里，我们可以看到的是，数学的美既是感官刺激的产物，来自对客观对象的表面特征的直觉反映，也涉及更深层次的主观意识活动，这种主观审美评判超乎原始的感官感受。但是，这些不同形式和不同层次的审美过程却也有相同之处：它们都和比例、对称、对比、规律、简单、变化、和谐、统一等这些从柏拉图、亚里士多德就被关注的审美特征有关。而且，这些审美特征并不仅仅出现在不同层次的数学的审美中，也在音乐、艺术、文学、自然科学的审美过程中无处不在。

人们很早就已经在讨论人的审美体验和这些属性的关系，甚至试图建立美感和这些属性之间的度量关系。最近二、三十年里，神经美学和计算神经美学的出现，正是这种探索的科技路线。而现在人工智能的进步，又让我们有了更多的期待。

其它作品