杨益民
对于音乐我几乎是一个白痴,但学数学的几乎都知道:世界上第一个发现音乐与数学关系的是古希腊哲学家和数学家毕达哥拉斯。仔细瞧,拉斐尔的名画《雅典学院》

注意到名画左下侧哪位秃头老者和他身旁为他支着黑板的小孩,以及那块黑板上的画了吗?

他就是古希腊著名哲学家和数学家毕达哥拉斯,那个小孩支着的黑板上画着一把琴。毕达哥拉斯正坐在那里专注地推算数学与音乐的协调关系,琴的结构可能对毕达哥拉斯的数学推算有着重要的意义。不是吗?
毕达哥拉斯还有一句名言:“万物皆数”。
英国著名哲学家和数学家罗素在其名著《西方哲学史》中说:“一个只能显示于理性,而不显示于感官的永恒世界,全部的这一观念都源自于毕达哥拉斯。”
好一个“万物皆数”!绝对是至理名言。因为万物之间只要有大小、长短、距离、运动、时间等,就都牵涉到数,本质上就都可以用数学来描述。
“万物皆数”!嗟乎!这里的“万物”当然也包含音乐啦!大哲学家、大数学家莱布尼茨也有句名言:“音乐是数学在灵魂中无意识的运算。”爱因斯坦也曾说:“我们这个世界可以由音乐的音符组成也可以由数学公式组成。”据说巴赫的音乐具有很强的“逻辑性”,巴赫因此被誉为音乐界的数学家。
贝多芬在他的大部分创作生涯中是在失聪中度过的,那他是如何创作出如此多错综复杂且美妙动人的乐曲的呢?似乎答案就在这些美妙音符背后隐藏的数学规律中。贝多芬曾说:作曲时,我脑海里总有一副图画,我就按照图画中的曲线来谱曲。
哲学家、数学家、音乐家为何都有这样的感觉与认识呢?
一、数学与音乐的共同特点的与联系
首先,数学与音乐的都具有高度的抽象性。它们各自有一套抽象的符号体系,通过抽象的独特符号语言来表达人类对世界的感知、认识与激情。
很多人认为数学和音乐似乎位于人类精神的两极,一个严谨,一个浪漫。其实数学与音乐都同时兼有严谨与浪漫的特质。音乐是及其严谨的艺术,而数学也并非像一般人认为的那样单调枯燥冷漠,而是与音乐一样充溢着激情、想象与幻想。
其次,乐器的制造和音乐本身都涉及到复杂的力学和声学等许多学科,这些学科本质上都可以通过数学来描述。弦或键的振动产生的波,本质上讲总可以用周期函数、傅立叶变换、波动方程、或别的什么数学物理理论来描述。
我们可以将乐谱子上的音与钢琴上的琴键做一个一一映射,写出两者之间的数学关系;至于不同音程不过是隔几个钢琴黑白键,也可以写出数学关系式。毫无疑问,不同音符与频率之间,以及拨弦的位置与频率之间也必然存在数学关系,这些频率或许构成一个等比数列,或其它的什么数学序列。按照这些数学序列,你或许也可以演奏出大致和谐的音乐呢!
声音由物体的振动产生,振动的强弱体现为声音的大小,不同物体的振动体现为声音的不同音色,而振动的快慢就体现为声音的高低。
振动的快慢在物理学上用频率(单位赫兹)表示。音乐中常使用的频率范围大约是16—4000赫兹,而人声及器乐中最富于表现力的频率范围大约是60—1000赫兹。钢琴中央C“do”的频率为261.63赫兹。
据说毕达哥拉斯发现:一根空弦发出的声音与同一根半长的空弦发出的声音有非常和谐(协和)的音效。后来这两个音被称为具有“如影随形”的八度音的关系。除非两音频率完全相等,八度音在听觉和谐方面关系最为密切。
18世纪初英国数学家泰勒(1685-1731)获得弦振动频率公式:
f =(1/(2l))√(T/ρ)
其中:l 表示弦的长度,T表示弦的张紧程度,ρ表示弦的密度。
从此公式可知:对于同一根弦其频率与弦长成反比,一对八度音的频率之比等于2∶1。
乐音体系中各音的绝对准确高度及其相互关系叫做音律。其中最主要的有“纯律”、“五度相生律”和“十二平均律”。目前世界各国采用最广泛的是“十二平均律”。
半音是十二平均律中最小的音高距离,两个半音的距离为全音。人们注意到五度律十二声音阶中的两种半音相差不大,如果消除这种差别对于键盘乐器的转调将是十分方便的,因为键盘乐器的每个键的音高是固定的,而不象拨弦或拉弦乐器的音高由手指位置决定。消除两种半音差别的办法是使相邻各音频率之比相等,“十二平均律”就是将八度分成十二个均等的部分——半音——的音律。即八度内包括十二个半音,也就是六个全音。
于是,我们可由如下算式:
A×B×B×B×B×B×B×B×B×B×B×B×B=2A
求得:十二平均律中任何相邻两音频率之比均为B=12√2
从而十二平均律构成的音阶如下:
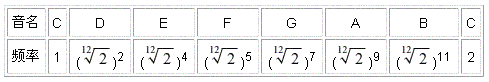
其中:E到F,B到C是半音,其余相邻两音间的距离都是全音。在钢琴上,即为:相邻两个琴键(包括黑键)构成半音,隔开一个琴键的两个音都构成全音。
毕达哥拉斯发现了弦振动产生的音律与弦长的关系,以及音律和谐的规律。毕达哥拉斯的这个和声学定律,通常被认为是人类历史上, 发现自然规律,并用数学术语来表达物理世界的第一个范例。
毕达哥拉斯的另一得意之作是他的 “百牛定理”——勾股定理。之所以称为“百牛定理”,是因为毕达哥拉斯学派杀了一百头牛来庆祝这个定理的发现。

已知正方形的边长为1,问其对角线有多长?这个问题对古巴比伦人、古埃及人、古印度人、古华夏人是根本不用费心的小菜一碟。因为这些远古文明都不懂得用逻辑演绎来得出一般性结论,而是只满足于实际应用。
对此类问题,他们都是通过测量计算来给出答案,例如巴比伦人计算出这个值为1.4142129。这个值是√2相当精确的近似。但这样通过测量计算得出的答案永远不可能是无理数√2,只能是有理数(√2截尾后的数)。
无理数√2的发现对于毕达哥拉斯学派和古希腊人来说,却是最感头痛的问题,这引起了他们巨大的精神创伤,以及数学、宗教和哲学方面的危机。
前面我们讲到毕达哥拉斯学派哲学思想的核心是“万物皆数”,但是,当时他们所说的“数”是自然数和整数与整数之比——有理数。
我们必须强调:因为无理数是无穷不循环小数,因此任何的测量工具和归纳方法都不可能得到无理数,无理数只可能通过演绎推理得到。毕达哥拉斯学派认为“数”就是整数和有理数就一点也不奇怪了!实际上,除古希腊以外,其它不重视或不明白演绎推理力量的古文明也没有发现无理数,这也是必然的结果了!
当毕达哥拉斯的学生利用他最为得意的“百牛定理”证明了√2不能表现为整数之比(有理数)时,毕达哥拉斯学派陷入了惶恐。无理数的存在性与不可公度性的发现,以及有理数无限稠密,但它并不能覆盖整个直线,在毕达哥拉斯学派内部引起了极大震动,这是对毕达哥拉斯哲学思想核心的致命一击。
毕达哥拉斯学派的哲学和数学的基础轰然倒塌了,并由此爆发了人类思想史上的“第一次数学危机”。这个“逻辑上的丑闻”是如此可怕,以致于毕达哥拉斯学派规定必须对此严守秘密,并将其发现者灭口了。
毕达哥拉斯学派发现了音律与数学的基本关系与规律,及无理数。却不敢承认无理数的存在。谁知如今十二平均律中任何相邻两音频率之比却均为无理数12√2。毕达哥拉斯学派发现,而不愿承认的无理数,居然进入了他所研究的数学与音乐的关系中,这真是与他开了一个天大的玩笑!真是一件令人惊异,又遗憾的事!
坚持演绎推理是数学证明中唯一可靠的方法,是古希腊人对人类文明的最为重要的贡献之一。它使数学从木匠的工具盒、农民的小草棚和测量员的背包中解放出来,使数学从经验科学中解放出来,形成了演绎逻辑的思想体系,揭示了人类理性力量的至高无上的重要性。
在这以后,人们开始靠理性思维,而不是只靠感官思维与合情思维去判定什么是正确的。正是依靠这种判断,理性的逻辑演绎方法,才为西方文明开辟了道路,在人类文明史上产生了巨大的影响。
“万物皆数”,音乐与数学间也必然存在着内在的各种联系,这是毫无疑问的!
二、数学与音乐的不同
事实上,不管有多少数学家、科学家怎么说,也不管你可以用什么数学物理理论来描述数学与音乐的关系,但毫无疑问音乐的本质还是音乐,而非数学。何也?
数学和音乐最大的不同,恰恰在于数学引以为傲的量化精确性和逻辑严谨性上。数学推理来不得一丝一毫的不严谨。作曲家虽然也会精心安排每个音符,但绝不可能如数学家推理那么严谨。音乐大师也不可能仅仅是一点不错的对谱弹奏。
同样的曲谱,不同的音乐家却能演奏出不同风格,绝没有最佳的标准答案。面对同一首作品,经过严格专业训练的音乐人,可能都能准确的弹出每一个音符,但有多少能成为音乐大师呢?
按照曲谱你或许也可以演奏出和谐的音乐。但音乐家对不和谐音的应用,常常同样充满魅力,令人神往。换言之,音乐家在曲谱的确定性当中,增加了个人的理解、感觉、技巧、激情和创造力等。创造了人类其他语言所不能,也无资格唱颂的独特之音。
因此,尽管我们可以研究乐章背后的数学规律,但当旋律以某种形式呈现的时候,能够如此深入人心,绝对不仅仅是它符合数学的某个规律。其间的奥妙很多时候只能意会,而不能言传。数学可没有什么只能意会而不能言传的东西!只有你听不懂、弄不明的坚深。
贝多芬的魅力和真正的音乐天赋,不仅在于他脑海里总有一副图画,按照图画中的曲线来谱曲。更在于他对音乐的超强感知力、辩识力和创造力。
三、结束语
“万物皆数”,但不唯数!每门科学和艺术自有自身的特点。
音乐是人类心灵深处灵魂的表白和倾诉,没有半点矫揉造作,没有虚伪和掩饰;而数学则以它的逻辑严谨和确切无误的推理,深刻地反映大千世界的运行规律和模式。也许音乐被描述为有感情的数学有些牵强,但是数学或许可以是理性的音乐。音乐家可以感知数学,数学家能够欣赏并思考音乐。
我们知道现在利用计算机技术,可以把一些数学公式直接变成漂亮的、具有复杂图案的、五彩纷呈的图形。计算机音乐则可以奏出各种随你想象的音乐。或许随着科学技术与数学理论的发展,艺术会越来越科学化,科学也会越来越艺术化,两者曾在山麓分手,有朝一日,或许又将会在山顶重逢。谁又说得清呢?
至于说有没有可能,在人工智能和大数据算法支持下来进行音乐创作呢?当然可能,事实上,现在已经有这样的音乐存在。
美国数学物理学博士,计算机教授道格拉斯.霍夫斯塔特曾在《哥德尔、艾舍尔、巴赫:集异璧之大成》中预言,将来可能会出现一些人工智能的机器,会跨越数理逻辑、绘画和音乐等这些看起来毫不搭界领域的临界点。最终,人工智能能够自我感知、自我创造、自我参照。当前他的这些预言正在逐步实现。
这背后的根本推手,不会是别的,必然是数学!“万物皆数”理当成为我们的绝对信条。
注:明太祖朱元璋第八世孙朱载堉制十二平均律,较之巴赫更早。朱载堉用算盘计算出十二平均律的那个公比12√2的近似值,精确到小数点后25位。朱载堉不仅制作了十二平均律,而且据此实际制造出了相应的律管以及弦乐器。
谢谢同窗龙冰提供的“注”中的这个补充。
No post found!

